Packaging materials
The market for fibre based packages has been growing for several decades and this growth is expected to continue. The success of packages based on cellulose fibres is to a large extent due to the lightweight, low cost and excellent recyclability of the material. A unique feature of fibre based packages, e.g., paperboard, is their ability to easily fold. This feature stems from the highly anisotropic properties, e.g., the in-plane versus the out-of-plane properties. The strength of a paperboard can be magnitudes larger in the in-plane compared to the out-of-plane direction.
The process of converting paperboard into a package is a seemingly simple process. This is, certainly not the case, as paperboard possesses many challenging features such as: elastic and plastic anisotropy, strain rate effects, large plastic deformation, degradation (damage), moisture and temperature dependence. The complexity of the material is attributed to the fact that a paperboard consists of complex layered fiber network, cf. the figure below. In contrast to, e.g., a sheet metal which, at the engineering scale, can be considered as isotropic, paperboard is far from being isotropic, thus the understanding of the underlying mechanisms, as well as adequate models, is key for an effective and reliable product development.
A difficulty associated with converting paperboard into liquid packages is to produce high quality packages in a rapid, repeatable manner. Small fluctuations in the environment parameters in any stage of the converting process, including temperature, moisture and variations in base material, can lead to severe defects in the final product. The converting process typically involves multiple steps of creasing, folding and, finally, filling. During folding, tensile and compressive stresses will arise due to the bending and, in the initial folding of paperboard, shear bands will develop that later lead to delamination and formation of wrinkles. Wrinkles will change the curvature and consequently increase the stresses, which might contribute to the development of in-plane cracks. Such, in-plane board surface cracks in a liquid package may jeopardize the integrity of the package. Therefore, the control of crack initiation and propagation is of key importance.
General research approach
Developments of the mechanical models packaging materials for require detailed understanding of the controlling deformation mechanisms and microstructures, which, in turn, requires new experimental methods. However, the experimental characterization of paperboard that has been subject to creasing and folding processes is not a trivial task. The difficulties stem from the fact that only small specimens can be investigated, i.e. the thickness of the board defines the size of the area of interest. Moreover, the microstructure of paper materials is extremely complex and consequently difficult to characterize. Mechanically, the folding and creasing process is frequently characterized via macroscopic, measurements such as force-compression response for creasing and moment-rotation response for folding. Although such measurements can provide information about mechanical behavior, they do not reveal any information about processes active at lower scales, in particular, the microscale. Greater understanding of the structure and interaction of the fibre network can be achieved using x-ray tomography.
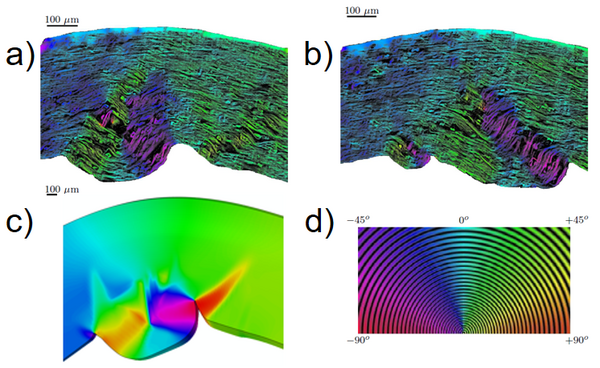
To illustrate the complex deformation modes and microstructural interactions that can occur during the converting process, the figure below shows the delamination at different cross sections through a paperboard sample after a folding process. Using modern experimental facilities at the 4D Imaging Lab (LTH), 3D images from x-ray tomography have revealed information regarding the underlying deformation mechanisms that were previously not accessible.
A few examples
Simulation of a 3d creasing process
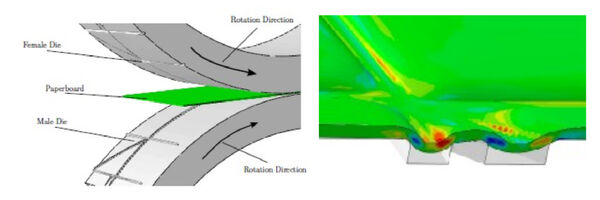
An elastic-plastic 3D-continuum model for paperboard has been developed by Borgqvist et al. (2011-2016) at the Division of Solid Mechanics, Lund University. The model is today sufficiently robust for effective simulation driven product development. Furthermore, the model is implemented as a user material routine in the commercial finite element codes Abaqus and LS-Dyna and is currently being used by industry in development projects. The model is used for simulations of both laboratory creasing with straight-line crease tool and industrial rotative creasing in 3D (cf. figure below), as well as forming simulations in filling machines to identify machine and material interactions between different machine designs and/or package material parameters.
In contrast to competing numerical simulation tools, the model developed by Borgqvist and co-workers is able to simulate complex deformation patterns. Previous models are to some extent able to capture the overall mechanical response, however, since initiation of cracks and defects are, by nature, local phenomena, models that can resolve the local behaviour are essential.
Numerical and experimental study of the Relative Crease Strength (RCS)
The (RCS) value is frequently used in the industry as a quality measure of paperboard ability to fold into a package. The RCS value is related to the reduction of the bending moment due to a creasing operation. To gain understanding of the underlying mechanisms, the RCS process has been simulated and compared to experiments. Example results from experiments and numerical predictions are shown in the figure below and the correlation of the two goes far beyond that which might be obtained with previous numerical models.
Even though the Borgqvist model has been used to improve real production processes, the model still lacks the capability to account for viscosity and through-thickness variations, for example. Consequently, the mechanics of fibre microstructure and how it should be incorporated in numerical models still needs significant research.
Propagating defects in packaging materials
Since the nucleation and propagation of cracks are of paramount importance, the interplay between cracks and microstructure has been investigated. This can be seen in the figure below.
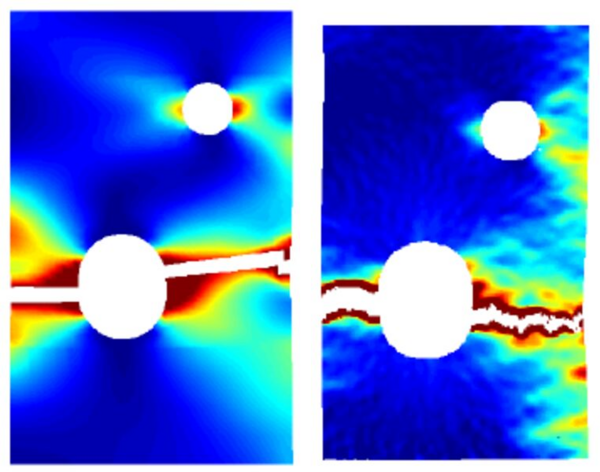
To further investigate the crack propagation properties, Vojskovic (2015) investigated the influence of fibre orientation on crack propagation. Initial results of this study are shown in the figure below. With this approach, cracks can propagate independently of the underlying finite element discretisation, thus enabling detailed study of crack processes.
Full forming simulation
In addition to adding to the understanding of local phenomena, numerical methods are valuable for the understanding of the interaction between filling media, tools and laminate during the converting process. Due to long-range effects, such as boundary conditions, and local stress concentrations, the computer power required for full-scale models is enormous if a traditional 3D finite element approach is taken.
Robertsson (2017) developed an approach that allows the Borgqvist model to be combined with solid shell finite elements specially tailored for simulation of complex anisotropic materials. This new element allows regions without complex local deformation to be modeled with a fraction of the cost of a traditional approach. This approach has been demonstrated in the modeling of a full folding, figure below. In this project will build on and extend such approaches to enable industry-applicable simulations for real production scenarios.
To further investigate the crack propagation properties, Vojskovic (2015) investigated the influence of fibre orientation on crack propagation. Initial results of this study are shown in the figure below, where the strain field in a sample of board with propagating cracks was measured in a laboratory experiment (by digital image correlation) and compared to numerical simulation using a simplified version of the Borgqvist model enhanced with X-FEM (extended finite element method). With this approach, cracks can propagate independently of the underlying finite element discretisation, thus enabling detailed study of crack processes.